by Welcome to an exploration of quadratic equations, an integral part of algebra and mathematics. In this article, we will delve into the world of quadratic equations, with a particular focus on the equation xΒ²-11x+28=0. Throughout this comprehensive discussion, we will uncover the general concept of quadratic equations, explore a range of methods to solve them, and conduct a deep dive into a specific case study to understand the practical applications of these equations.
Understanding Quadratic Equations xΒ²-11x+28=0
What is a Quadratic Equation?
To embark on this journey, we must first grasp the essence of a quadratic equation. A quadratic equation is a second-degree polynomial equation, characterized by the squared variable. The most fundamental form of a quadratic equation is expressed as:
ax^2 + bx + c = 0
In this equation, βa,β βb,β and βcβ represent coefficients, while βxβ stands for the variable. The equation xΒ²-11x+28=0 precisely aligns with this standard form.
General Form of a Quadratic Equation
Understanding the general form of a quadratic equation is pivotal as it underpins the foundation of these equations. By recognizing this structure, we can conveniently identify the coefficients βa,β βb,β and βc.β For our specific equation, βaβ is 1, βbβ is -11, and βcβ is 28.
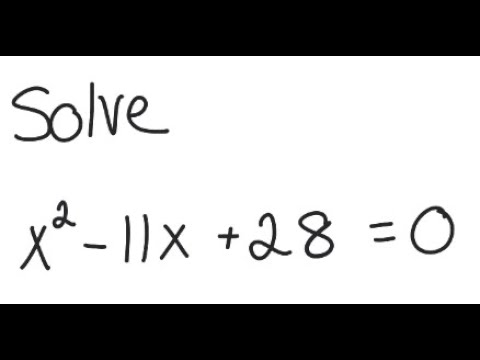
Solving Quadratic Equation xΒ²-11x+28=0
Quadratic equations are a realm of mathematical problems that can be tackled using various methods. Letβs explore two prominent techniques:
Factoring
Factoring is a method employed to solve quadratic equations that can be be easily broken down. However, for equations as complex as xΒ²-11x+28=0, factoring may not be the most straightforward approach.
Quadratic Formula
The quadratic formula emerges as a versatile and universally applicable approach to solving quadratic equations. This formula, often called upon, is:
x = (-b Β± β(b^2 β 4ac)) / 2a
With this formula, we obtain the roots of the equation, representing the values of βxβ that render the equation equal to zero.
x^2-11x+28=0: A Case Study
Intriguingly, we now turn our attention to the specific equation x2-11x+28=0. Our exploration will involve a step-by-step analysis using the quadratic formula.
Step 1: Identifying the Coefficients
To initiate this journey, we must first identify the coefficients. In the equation at hand, βaβ is 1, βbβ is -11, and βcβ is 28.
Step 2: Applying the Quadratic Formula
With the coefficients now in our grasp, we can proceed to apply the quadratic formula. The equation takes shape as follows:
x = (-(-11) Β± β((-11)^2 β 4 * 1 * 28)) / (2 * 1)
In the pursuit of a solution, we simplify the equation, leading to:
x = (11 Β± β(121 β 112)) / 2
x = (11 Β± β9) / 2
Step 3: Finding the Roots
As the equation begins to crystallize, we uncover two potential solutions:
- x = (11 + 3) / 2 = 7
- x = (11 β 3) / 2 = 4
Thus, the roots of the equation x2-11x+28=0 are revealed as x = 7 and x = 4.
Must Read: 4x ^ 2 β 5x β 12 = 0
Graphical Representation of Quadratic Equations
In the realm of quadratic equations, the graphical depiction often takes the form of a parabola. This U-shaped curve provides vital insights into the behavior of these equations, with the vertex being a central point, signifying either the minimum or maximum of the parabola.
Applications of Quadratic Equations
The practicality of quadratic equations transcends theory, finding applications in diverse domains such as physics, engineering, and economics. In these real-world scenarios, quadratic equations serve as powerful tools to model and resolve problems with precision.
Conclusion
To sum up, delving into the realm of quadratic equations has been a fascinating journey. In this article, we have unraveled the fundamental concepts surrounding quadratic equations, unraveled the methodology of solving them using the quadratic formula, and witnessed the practical implications through a specific case study, namely x2-11x+28=0. Furthermore, we have explored the visual representation of quadratic equations via parabolic graphs and highlighted their real-world relevance in various applications.
